【线性表基础】基于线性表的简单算法【Java 版】¶

本文描述了基于线性表的简单算法及其代码【Java 实现】

1-1 删除单链表中所有重复元素¶

    // Example 1-1 删除单链表中所有重复元素
    private static void removeRepeat(LinkList L)
    {
        Node node = L.head.next; // 首结点
        while (node != null) // 一重循环，遍历L中的每一个元素
        {
//          Object data=p.data;
            Node p = node; // q结点的前驱
            Node q = p.next; // 与node数据相同的结点
            while (q != null) // 二重循环，寻找相同结点
            {
                if (node.data.equals(q.data))
                {
                    p.next = q.next; // 删除q结点
                } else
                {
                    p = p.next; // 不相同时p结点后移，相同时p待在原位等待下一次比较
                }
                q = q.next; // 无论相不相同q结点都要后移
            }
            node = node.next;
        }
    }

第二种方法：

    // Example 1-1 书本代码
    private static void removeRepeatElem(LinkList L) throws Exception
    {
        Node p = L.head.next, q; // p为首结点
        while (p != null)
        {
            int order = L.indexOf(p.data); // 记录下p的位置
            q = p.next;
            while (q != null)
            {
                if (p.data.equals(q.data))
                {
                    L.remove(order + 1); // order+1即为q结点的位置
                } else
                {
                    ++order; // 使得每次order都是q结点的前驱
                }
                q = q.next;
            }
            p = p.next;
        }
    }

1-2 删除单链表指定结点¶

删除所有数据为 x 的结点，并返回数量，算法思想与 1-1 差不多

    // Example 1-2 删除所有数据为x的结点，并返回数量，算法思想与1-1差不多
    private static int removeAll(LinkList L, Object x)
    {
        Node p = L.head;
        Node q = p.next;
        int count = 0;
        while (q != null)
        {
            if (q.data.equals(x))
            {
                p.next = q.next;
                count++;
            } else
            {
                p = p.next;
            }
            q = q.next;
        }
        return count;
    }

测试我们的两种算法的结果：

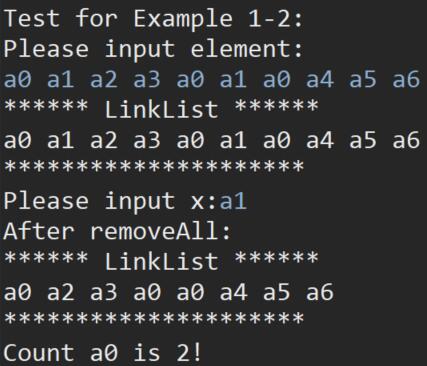
算法 1-1：

算法 1-2：

2-1 顺序表的就地逆置¶

试写一算法，实现顺序表的就地逆置即利用原表的存储空间将线性表（a1,a2…,an）逆置为（an,an-1…,a1）

    // Example 2-1 实现对顺序表的就地逆置
    // 逆置：把(a1,a2,......,an)变成(an,an-1,...,a1)
    // 就地：逆置后的数据元素仍存储在原来的存储空间中
    private static void reverseSqList(SqList L)
    {
        for (int i = 0; i < (int) (L.curLen / 2); i++)  // 确定循环次数，偶数为长度的一半，奇数为长度减一的一半，因此取curLen/2的整数
        {
            //下面三个语句实现就地逆置
            Object temp = L.listItem[i];
            L.listItem[i] = L.listItem[L.curLen - 1 - i];
            L.listItem[L.curLen - 1 - i] = temp;
        }
    }

2-2 单链表的就地逆置¶

实现对带头结点的单链表的就地逆置

    // Example 2-2 实现对带头结点单链表的就地逆置
    private static void reverseLinkList(LinkList L) throws Exception
    {
        Node p = L.head.next;
        L.head.next = null;
        while (p != null)
        {
            Node q=p.next;  // q指向p的后继，保留住后续结点
            // 下面两个语句实现头插法，将p插入在位置为0的地方
            p.next=L.head.next;     // p的后继指向首结点
            L.head.next=p;  // 首结点指向p
            p = q;  // p重新指向后续结点
        }
    }

测试结果：

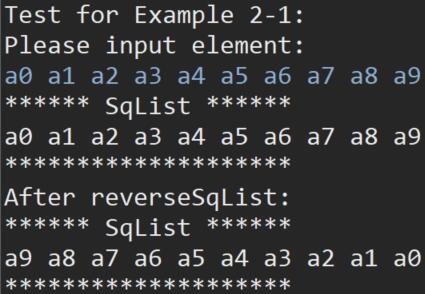
算法 2-1：

算法 2-2：

3-1 有序单链表中插入元素¶

实现在非递减的有序整型单链表中插入一个值为 x 的数据元素，并使单链表仍保持有序

    // Example 3-1 实现在非递减的有序整型单链表中插入一个值为x的数据元素，并使单链表仍保持有序
    private static void insertOrder(LinkList L, int x)
    {
        Node p = L.head.next; // 首结点
        Node q = L.head; // p的前驱
        while (p != null && Integer.valueOf(p.data.toString()) < x) // 当结点p的值大于等于x时跳出while
        {
            q = q.next;
            p = p.next;
        }
        Node s = new Node(x);
        s.next = p;
        q.next = s;
    }

3-2 合并有序链表¶

实现将两个非递减链表 LA 和 LB 合并排列成一个新的非递减链表 LA

    // Example 3-2 实现将两个非递减链表LA和LB合并排列成一个新的非递减链表LA
    private static LinkList mergeList(LinkList LA, LinkList LB) throws Exception
    {
        Node pa = LA.head.next; // LA首结点
        Node pb = LB.head.next; // LB首结点
//      LA.head.next = null; // 置空LA链表，这话写与不写都不影响插入
        Node tail = LA.head; // 指向新链表LA的最后一个结点
        while (pa != null && pb != null)
        {
            // 使用尾插法，按照非递减顺序插入，并且不需要插入时不需要将pa或pb指向null，因为最后插入的结点一定是null
            if (Integer.valueOf(pa.data.toString()) < Integer.valueOf(pb.data.toString()))
            {
                // 若pa.data小于pb.data则将pa插在尾结点后，并且继续比较pa后续结点，直到出现大于等于pb的结点为止
                tail.next = pa;
                tail = pa; // tail后移
                pa = pa.next; // 使得pa重新指向后续结点
            } else
            {
                // 若pa.data大于等于pb.data则将pb插在pa的前面，并且继续比较pb后续结点，直到出现大于pa的结点为止
                tail.next = pb;
                tail = pb; // tail后移
                pb = pb.next; // 使得pb重新指向后续结点
            }
        }
        tail.next = (pa != null ? pa : pb);
        return LA;
    }

测试结果：

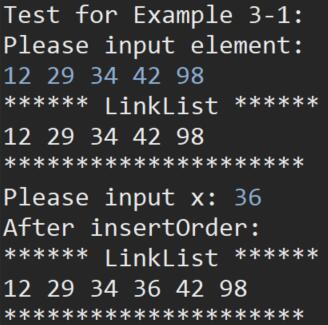
算法 3-1：

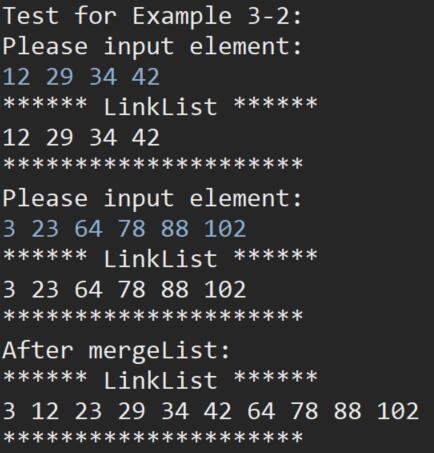
算法 3-2：

以上便是基于线性表的简单算法，此系列后面会陆续介绍更多有关数据结构的内容，也会更新一些关于数据结构的算法题目例子，谢谢大家支持！